数据和特征的质量决定了机器学习的上限。
特征工程包括:
特征处理包括1. 特征清洗,2. 数据预处理。
主要任务是对异常样本的处理。对”异常“的定义并不统一,简单起见,离群点是会被认为为异常点的。在统计上离群点往往和低概率相关联,以下方法都是以概率思想识别离群点:
箱型图分析:根据其四分位数,计算极差以及分位差(思想:找出离密度高的群体较远的点)
一般认为:如果数据量足够大,1/4和3/4分位差之外的数据可以认为是异常点。如果数据量不够大,则认为$(D_{\frac{1}{4}}-1.5\times(D_{\frac34}-D_{\frac14}), D_{\frac{3}{4}}+1.5\times(D_{\frac34}-D_{\frac14})$的之外的数据为异常数据。
正态图分析:$3\sigma$原则
基于统计的方法的缺点是:1. 非常依赖于数据集的数据分布,数据集中的数据是否满足某种分布对效果影响很大,2. 离群点的意义有多种。
一般来说可以在初期尝试使用这些方法,观察模型效果是否提升。
它是基于相似度衡量的模型的一种,异常点和正常点的分布不同,因此二者的相似度低。
主要思想是:对于每个点计算它的k近邻距离,一般认为异常点的第k邻距离更大。所以在计算时,就是先计算出每个点的k近邻距离,然后进行排序,选择距离最大的几个为异常点。
它受数据维度的影响比较大,当维度比较低的时候表现很好。事实上基于距离的方法在高维时表现都不佳。
思想:找出分布稀疏且离密度高的群体较远的点。
它只能给出是不是异常点,不能量化每个数据点的异常程度。
基于密度的LOF算法要更简单、直观。它不需要对数据的分布做太多要求,还能量化每个数据点的异常程度(outlierness)。
Local Outlier Factor (youth-49.github.io)
Python机器学习笔记:异常点检测算法——One Class SVM - 战争热诚 - 博客园 (cnblogs.com)
【异常检测】孤立森林(Isolation Forest)算法简介 - 云+社区 - 腾讯云 (tencent.com)
对于未经处理的特征,可能存在以下问题:
与之对应地,有如下解决方法:
无量纲化
无量纲化包括对数据标准化,区间缩放,归一化。
标准化:使该特征符合均值为0,方差为1的分布:
\[x' = \frac{x-\overline x}{\sigma}\]区间缩放:使得数据等比例地缩放到一个给定区间:
\[x' = \frac{s-Min}{Max-Min}\]也修改了原数据分布的均值和方差,可以将标准化看作特殊的区间缩放。
归一化:归一化并不属于无量纲化的一种,归一化将每个样本的特征向量的模长变为1。
$L_p$归一化公式为:
\[x' = \frac{x}{(\sum_{i}^{n}x_i^p)^{\frac{1}{p}}}\]常采用$L_2$归一化。
二值化(离散化)
对某些特定任务,二值数据或离散化数据即可满足要求。连续实数值可能会造成信息冗余。一般的做法是设置阈值。
对定性特征进行one-hot编码或哑编码(Dummy coding)
为一种定性特征的每个取值设定一个定量值往往需要大量的专家知识和调参工作,通常的做法是采用one-hot coding或dummy coding的方式——假设有N种定性值,则:
one-hot coding:将这一个特征扩展为N种特征,当原始特征值为第i种定性值时,第i个扩展特征赋值为1,其他扩展特征赋值为0。
dummy coding:将这一个特征扩展为N-1种特征,将其中一种定性值编码为全0.
对于线性模型来说,使用one-hot编码或哑编码后的特征可达到非线性的效果。
Missing value
对缺失值的处理包括丢弃和填充。填充缺失值往往用该特征取值的均值。
数据变化
常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。
以上操作均可借助sklearn.preprocess库实现:
| 类 | 功能 | 说明 |
|---|---|---|
| StandardScaler | 无量纲化 | 标准化,基于特征矩阵的列,将特征值转换至服从标准正态分布 |
| MinMaxScaler | 无量纲化 | 区间缩放,基于最大最小值,将特征值转换到[0, 1]区间上 |
| Normalizer | 归一化 | 基于特征矩阵的行,将样本向量转换为“单位向量” |
| Binarizer | 二值化 | 基于给定阈值,将定量特征按阈值划分 |
| OneHotEncoder | 哑编码 | 将定性数据编码为定量数据 |
| Imputer | 缺失值计算 | 计算缺失值,缺失值可填充为均值等 |
| PolynomialFeatures | 多项式数据转换 | 多项式数据转换 |
| FunctionTransformer | 自定义单元数据转换 | 使用单变元的函数来转换数据 |
对于文本特征,将自然语言预处理成向量,一般有如下方法:
统计每个词的词频并归一化(防止倾向于长文档):
\[TF(w_i) = \frac{count(w_i)}{\sum_jcount(w_j)}\]然后筛去出现频率高且与主题相关性低的词,同时增加与主题相关性强的词的权重:
\[IDF(w_i) = log(\frac{语料库中文档总数}{包含w_i的文档数+eps})\]eps是防止分母为0的,一般取1。
定义TF-IDF为:
\[TF-IDF = TF \times IDF\]相比于之前的词袋模型,TF-IDF显著降低了普遍出现的词的权重(如的,了,是),增加了有标志性词的权重。在文档的关键词提取中,按照TF-IDF值排序,靠前的可以视为文章的关键词。
TF-IDF的优点是简单快速,缺点是上述对”重要性“的定义不够全面,可能不能适应一些情景。另外,该方法假设了词之间的独立性,缺少语义信息。
还有一种预处理方式是组合特征,如借助GBDT+LR:先用GBDT训练模型,得到解释性良好的特征集合,再将组合特征与原特征一起训练。
特征选择的目的是选出对任务有意义的特征输入机器学习模型,通常要考虑特征的:
对特征评分,设置阈值,选择高于(或低于)阈值的特征。
这种方法的缺点是假设了特征的独立性,有可能将有用的关联特征也过滤掉。
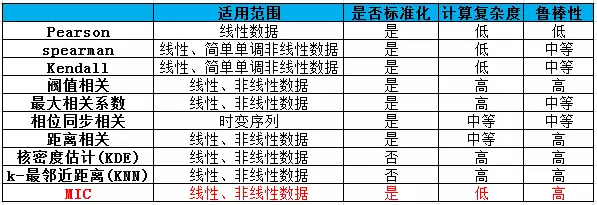
对于分类问题,可采用卡方检验和互信息法。
对于回归问题,可以采用皮尔森相关系数和最大信息系数。
方差选择法
计算每个特征的方差,根据阈值选择方差大于阈值的特征。
相关系数法
先要计算各个特征对目标值的相关系数以及相关系数的P值。
给定一组样本数据$(X_i. Y_i)$:
\[COV(X, Y) = E[(X-E(X))(Y-E(Y))] = E(XY)-E(X)E(Y)\]协方差为正时,二者正相关,为负时负相关。为了消除随机变量取值的影响,除以标准差以单位化(值域为[-1, 1]):
\[\begin{align} r &= \frac{COV(X,Y)}{\sigma _X \sigma_Y} \\ &= \frac{\sum_{i=1}^n(X_i-\overline X)(Y_i-\overline Y)}{\sqrt{\sum_{i=1}^n(X_i-\overline X)^2}\sqrt{\sum_{i=1}^n(Y_i-\overline Y)^2}} \end{align}\]这种相关系数是线性相关系数,在非线性条件下表现可能不佳。
卡方检验
是一种假设检验,要给出显著性水平$\sigma$,也可以用其他检验如T-检验,Z-检验,要根据数据分布确定。
经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值,因变量有M种取值,考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距,构建统计量:
\[\chi^2 = \sum\frac{(A-E)^2}{E}\]其中A是实际值(实际频数),E是假设自变量与因变量独立时的理论频数。这个统计量用于衡量实际值和理论值的差异程度,包含了以下两个信息:
统计学-卡方检验与卡方分布 - 程序员大本营 (pianshen.com) (其中喝牛奶的例子有点错误)
互信息与最大信息系数
Mutual Information and Maximum Information Coeffient (youth-49.github.io)

根据目标函数,每次选择若干特征或排除若干特征。
(转)Wrapper 这一类特征选择方法,应该来说是比较科学的,但是也是非常耗时,工业界在生产环境中很少使用,非常耗时,也是一个 NP 复杂的问题,一般通过不断迭代,然后每次加入一个特征,来训练模型,使用模型评估比如 AUC 或者 MSE 等函数评估是否将特征加入到特征子集中。
递归消除特征法使用一个基模型来进行多轮训练,每轮训练后,移除若干权值系数的特征,再基于新的特征集进行下一轮训练。
sklearn官方解释:对特征含有权重的预测模型(例如,线性模型对应参数coefficients),RFE通过递归减少考察的特征集规模来选择特征。首先,预测模型在原始特征上训练,每个特征指定一个权重。之后,那些拥有最小绝对值权重的特征被踢出特征集。如此往复递归,直至剩余的特征数量达到所需的特征数量。
RFECV 通过交叉验证的方式执行RFE,以此来选择最佳数量的特征:对于一个数量为d的feature的集合,他的所有的子集的个数是2的d次方减1(包含空集)。指定一个外部的学习算法,比如SVM之类的。通过该算法计算所有子集的validation error。选择error最小的那个子集作为所挑选的特征。
先使用某些机器学习算法或模型进行训练,得到各个特征的权值系数,根据系数选择特征。有些机器学习方法本身就具有对特征进行打分的机制,或者很容易将其运用到特征选择任务中,例如回归模型,SVM,决策树,随机森林等等。
(1)回归模型
回归模型最终会训练出各特征的权重,组成一个回归方程,则可以根据回归方程中的权重进行筛选,剔除一些较小的权重。
(2)SVM
SVM最终的分界函数是由边界上的点(特征)决定的,也就是说这些特征是比较重要的,其它特征则可以结合业务情况进行相应的删减。
(3)决策树
决策树结点的构建顺序和特征的重要性有关,则可以根据情况将一些靠近叶子结点的特征进行删减。
(4)随机森林
随机森林进行特征重要性评估,可以借助oob估计,通过对特征引入噪音,如果模型效果降低,则说明该特征较为重要。
(5)GBDT
先计算单棵树中特征分裂后损失的减少值,然后计算出多棵树的均值,即可比较出特征的重要性。
(6)XGboost
XGboost是通过该特征每棵树中分裂次数的和去计算的,比如这个特征在第一棵树分裂1次,第二棵树2次……,那么这个特征的得分就是(1+2+…)。
(7)基于惩罚项的特征选择
L1正则化具有截断性,L2正则化具有缩放效应,所以我们可以很好的利用线性模型的两种正则化选择特征。使用L1范数作为惩罚项的线性模型(Linear models)会得到稀疏解:大部分特征对应的系数为0。即起到了减少特征的作用。
以上均可借助sklearn.feature_selection实现:
| 类 | 所属方式 | 说明 |
|---|---|---|
| VarianceThreshold | Filter | 方差选择法 |
| SelectKBest | Filter | 可选关联系数、卡方校验、最大信息系数作为得分计算的方法 |
| RFE | Wrapper | 递归地训练基模型,将权值系数较小的特征从特征集合中消除 |
| SelectFromModel | Embedded | 训练基模型,选择权值系数较高的特征 |
可能由于特征矩阵过大,导致计算量大,训练时间长的问题,因此降低特征矩阵维度也是必不可少的。常见的降维方法除了以上提到的基于L1惩罚项的模型以外,另外还有主成分分析法(PCA)和线性判别分析(LDA),线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点,其本质是要将原始的样本映射到维度更低的样本空间中,但是PCA和LDA的映射目标不一样:PCA是为了让映射后的样本具有最大的发散性;而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法,而LDA是一种有监督的降维方法。