
Website:聚类算法评估指标
指出DPC存在的问题:

SNNDPC提出:

作者认为DPC没有考虑邻域的信息,而SNN-DP通过利用KNN来结合领域的信息。并且提出了计算$\rho$和$delta$的新方式,使得稀疏簇的簇中心也能显著地从decision graph上突出出来。




在距离的计算中,SNN-DPC使用了补偿机制,使得在稀疏的簇中,$\delta$的值也可以较高。稀疏簇的簇中心即使密度底,较大的$\delta$也可以使这个簇中心从其他点中pop out。


在一些极端情况下,会出现一个点同时Inevitable Suborde to多个类别的情况。
This circumstance may occasionally partially affect the clustering result. To avoid it, we present some simple but useful methods here:
尽可能的保证每个点至多inevitable subordinate to一个点。

The overall process is still divided into three steps: calculation of $ρ$ and $δ$, selection of cluster centers and allocation of non-central points.



第一次allocation是将那些inevitable subordinate to某些点的样本进行分类,BFS,初始化一个包含所有聚类中心的队列,然后每次pop front,将inevitable subordinate to这个点的所有点归为该点的类别,并加入队列。\textbf{这样保证簇的扩张是从聚类中心开始向外的,避免了在DPC中存在的一个问题:由于簇的某一部分密度更高,这部分如果被错误归类,周围的点将接连被错误归类}。
第二次allocation是将那些没有inevitable subordinate to任何点的样本进行分类。这些点都possible subordinate to某个或某些点。算法是将遍历所有未分配的点,生成一张allocation matrix,点p的KNN中有点q,且如果q属于第m类,则在矩阵的p-th row和m-th column加1。遍历结束后找到矩阵中值最大的元素,设在矩阵的第i行第j列,则将第i个unallocated point分配给第j类。执行下一次循环重新计算allocation matrix。
这样对每个点的分配都是谨慎的,都尽可能的考虑了包括邻域在内的最多的信息。
Time Complexity:
Algorithm 2: $O(n^2)$
Algorithm 3: $O(\max(k,m)n^2)$
总体时间复杂度: $O(\max(k,m)n^2)$
空间复杂度: $O(n^2)$
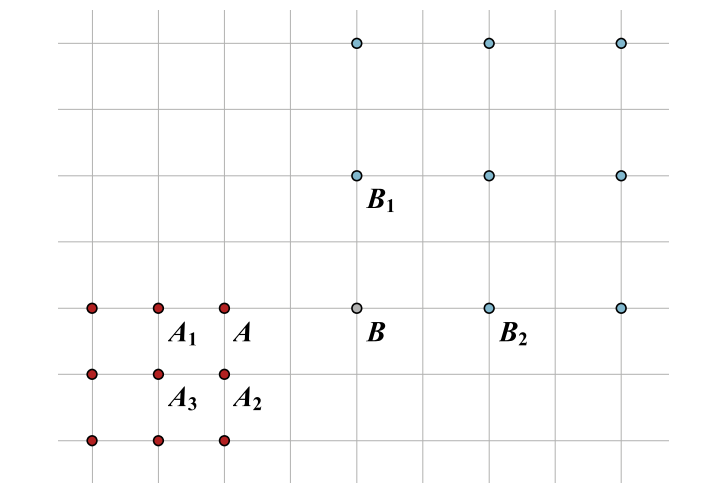
上面这个图解释了只依据据距离而出现的问题。DPC可能会将B点归为与A同一类,然后进而将B1,B2也归为和B同一类。如果考虑KNN的信息,计算A和B的SNN,发现它们并不inevitable subordinate to对方,说明二者共同的邻居很少。
DPC表现不佳的两个数据集:
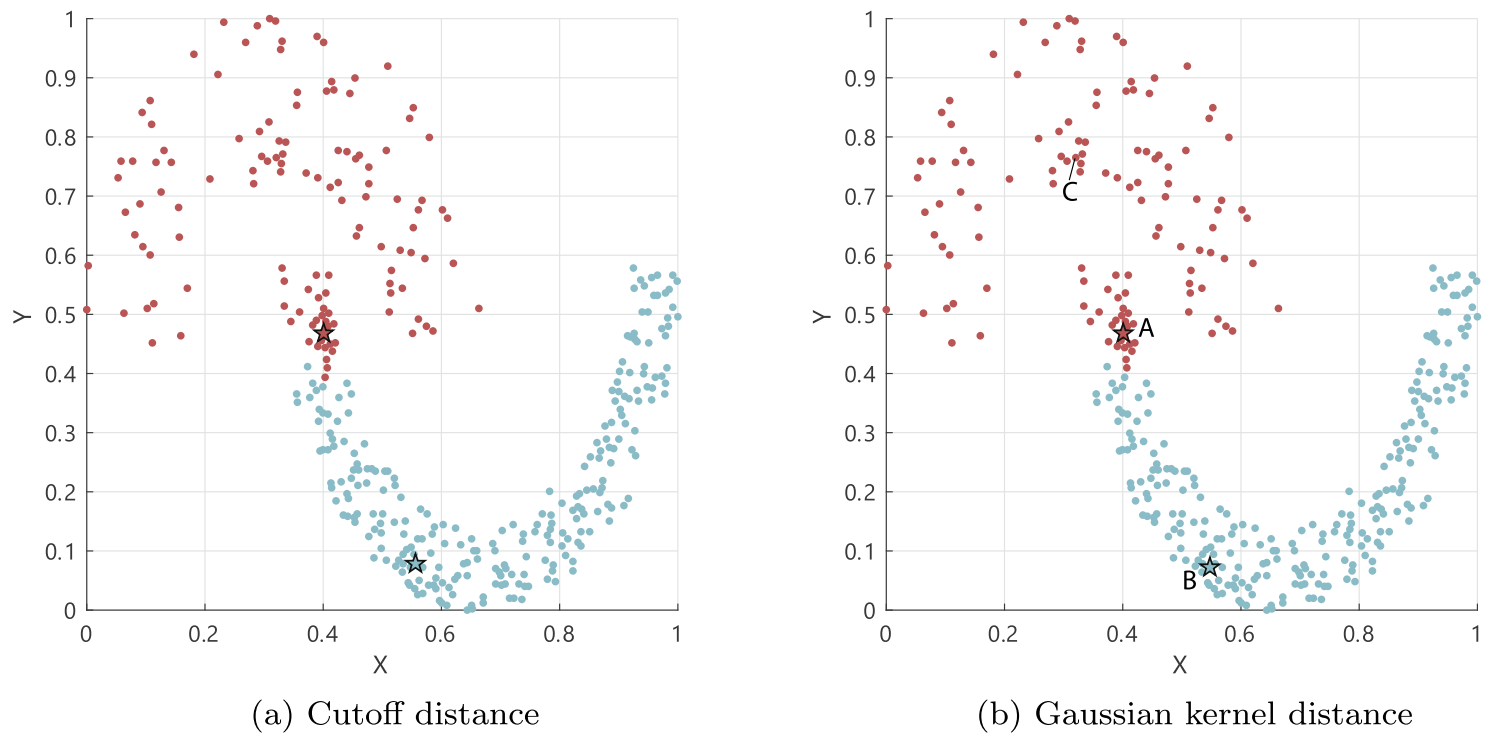
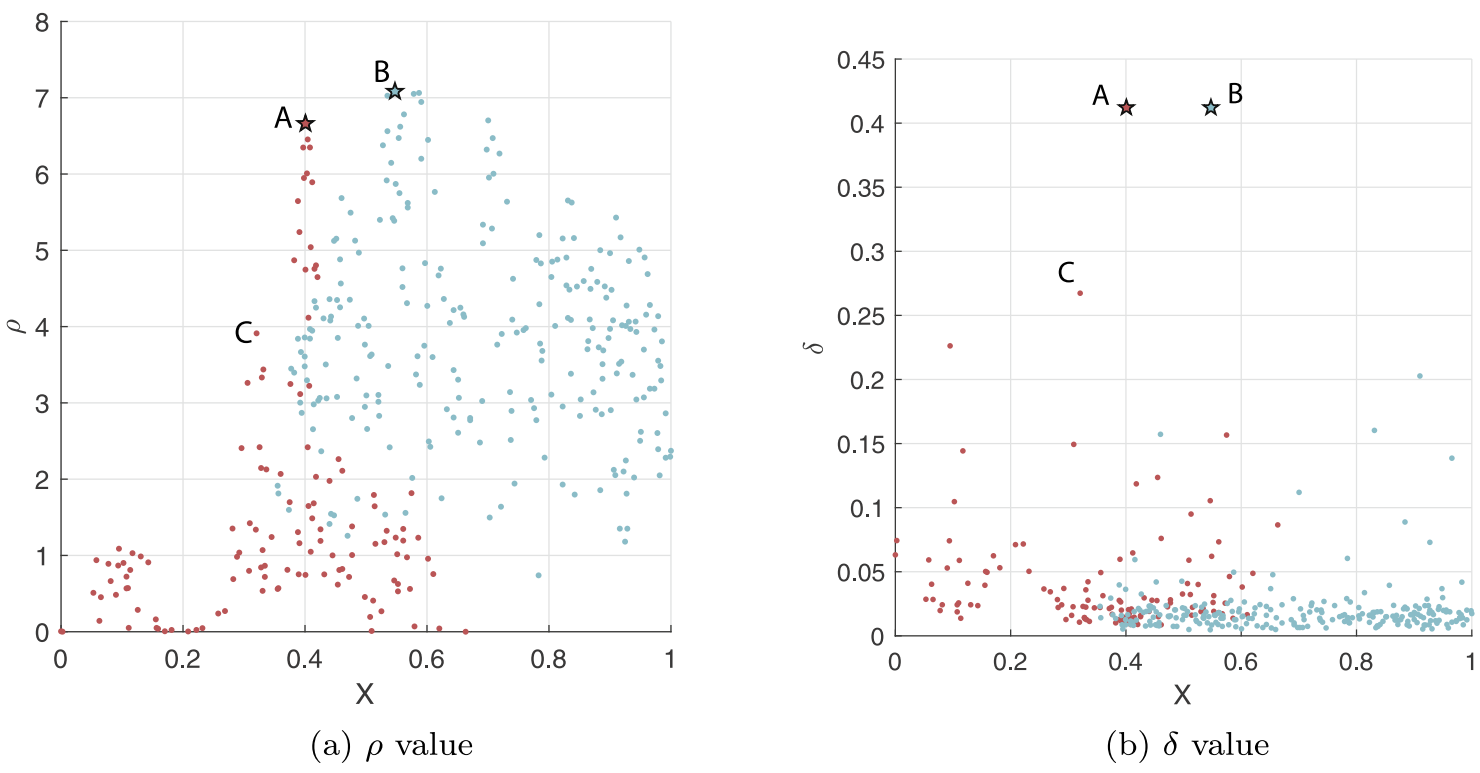
可以看出,DPC错误地将点A作为了一个聚类中心,因为点A密度大且距离最近的密度更高的点的距离也大,真正的聚类中心点C二者都比点A小。
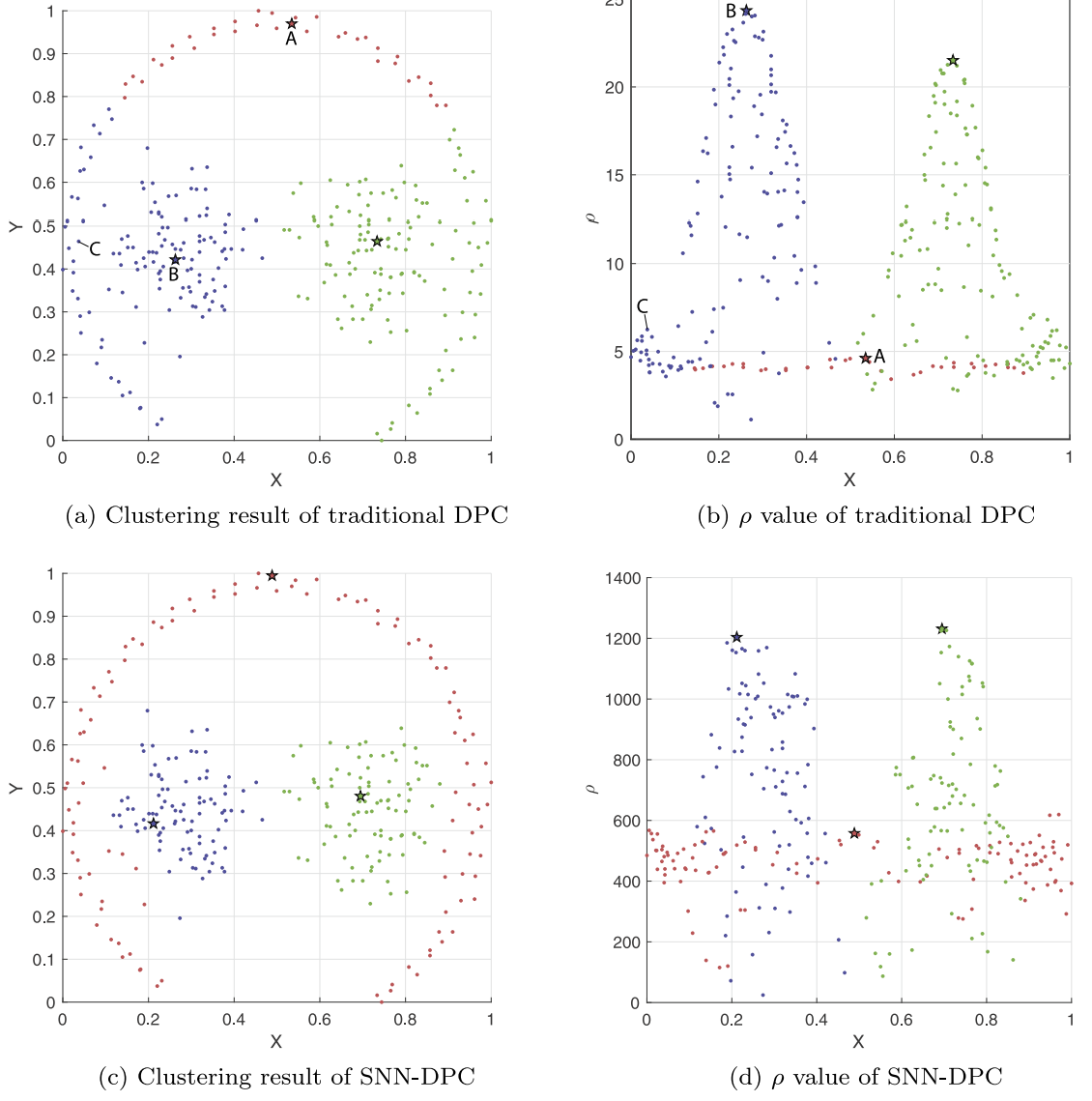
这个数据集反应了DPC在allocation中的不足。由于DPC是按照密度和距离最近的点的类别来分配,图中点C的密度比该簇中心(点A)更高,且离B所在的簇很近,DPC会将C以及周围的点都划分为B簇中的点。
而SNN-DPC的allocation遵循BFS的顺序,严格从聚类中心出发开始拓展,在一定程度上避免了分类错误和连续错误。