Clustering by fast search and find of density peaks
文章认为,聚类中心应具有以下特点:
密度大,即领域内点的数量多
与其他密度更大的点距离更远
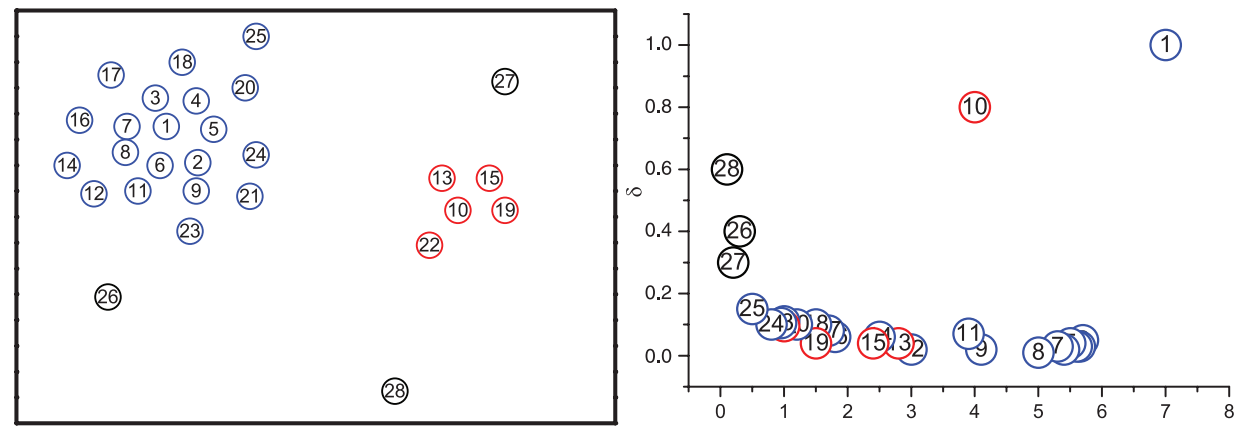
文章引入密度$\rho$和距离$\delta$的定义,利用decision graph找出聚类中心点,再将剩余的点指定为某一个聚类或噪声。
优点:克服了之前聚类算法只能发现类球状cluster的缺陷,且对数据分布空间的维数不敏感,在高维空间中也有良好的分类效果。可以避免离群点和噪音的干扰。
local density $\rho_i$, 有两种计算方法:
Cut-off kernel:
where $\chi(x) = 1$, if $x < 0$; $\chi(x) = 0$ otherwise.
Gaussian kernel:
\[\rho_i = \sum_j e^{-(\frac{d_{ij}}{d_c})^2}\]其中,Gaussian kernel得到的是连续值,上述两种方式都满足“在点i邻域内的点越多,$\rho_i$越大”。$d_c$是截断距离,需要预先指定。
对于$\rho$最大的点,我们定义:
\[\delta_i = \max_j (d_{ij})\]另一种定义: 设${q_i}{i=1}^N$是${\rho_i}{i=1}^{N}$的降序序列的下标序,满足: \(\rho_{q_1} \geq \rho_{q_2} \geq \cdots \geq \rho_{q_N}\) 则:
则:
\[\delta_i = \left\{ \begin{aligned} \max_{j\geq 2}(\delta_{q_j}) & & i = 1\\ \min_{j<i} (d_{q_iq_j}) & & i \geq 2\\ \end{aligned} \right.\]在原定义中,当点i具有最大local density时,$\delta$定义为离点i距离最远的点与点i的距离,否则,$\delta$为距离点i最近且local density更大的点离点i的距离。
这一做法的一个问题是,如果存在两个点i, j同属一个cluster,且local density相同且都较大,如果此时他们距离其他聚类中心的距离都较远(即$\delta$较大),则这两个点都会被作为聚类中心。但按照另一种定义,由于事先按照$\rho$排了序,排序算法会将其中的某一个排到前面,排到后面的那个点的$\delta$会小于等于被这两个点之间的距离,在decision graph中不会作为聚类中心。而且对于点$q_1$,$\delta = \max_{j\geq 2}(\delta_{q_j})$也已经足够大。
但是似乎也不是一定正确,有些情况下确实要按照原定义,将两个距离很近且local density很大的点作为两个聚类中心。

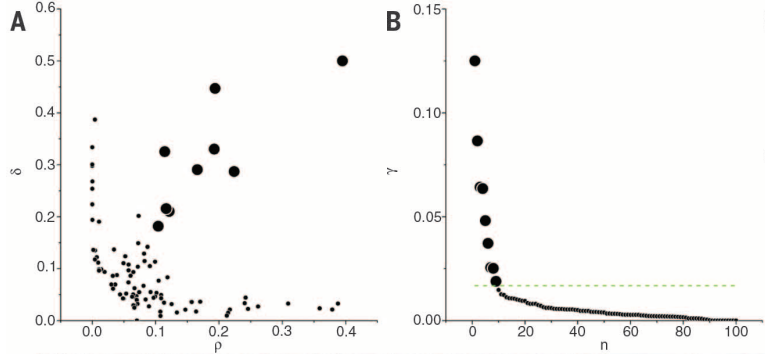
但是,需要主观地选择聚类中心,且decision graph有时很难确定某些点是否是聚类中心。文中给出一种方案:计算$\gamma_i = \rho_i \delta_i$,得到${\gamma_i}_{i = 1}^{N}$序列并以i为横轴,$\gamma$为纵轴画图,按$\gamma$从大到小选择若干个即可。“若干个”的选取依据:有聚类中心到非聚类中心有明显的突变。另外随机生成的点的$\gamma$应当符合power law。
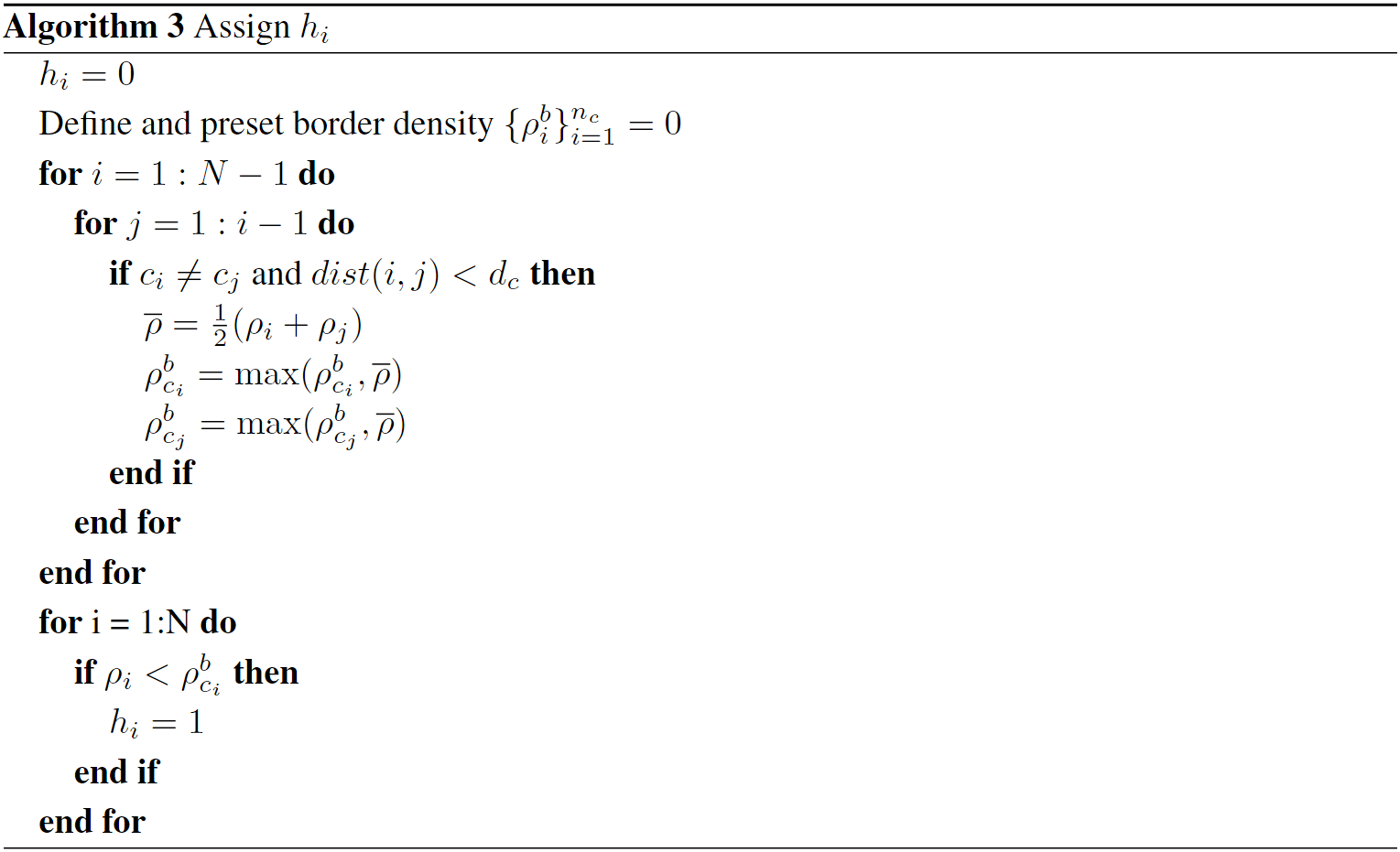
设数据集$S = {x_i}_{i = 1}^N$,有$n_c$个cluster。
${m_i}{i=1}^{n_c}$: 聚类中心的下标列,$x{m_i}$是第i个聚类的中心
$d_{max}$: 数据集中最远的两个点的距离。
${n_i}_{i=1}^N$: 比第i个点密度更大的点中离第i个点最近的点的标号,即:
\[n_{q_i} = \left\{ \begin{aligned} \mathop{argmin}_{q_j, j<i}(d_{q_iq_j}) & & i \geq 2\\ 0 & & i = 1\\ \end{aligned} \right.\]确定好聚类中心后,将使用$n_i$确定非聚类中心的归属。
${h_i}_{i=1}^N$: 标识该点是cluster core(=0)还是cluster halo(=1),文中指出cluster halo指聚类的边缘地带,local density较低。


论文中指出,$d_c$的选取应当使得每个点的平均邻居数为总数的$1\%-2\%$,可按如下方式选则$d_c$: 1. 对所有距离排序得到升序序列${d_i}_{i=1}^M$,2. 令$0.01 < percent < 0.02$,取升序序列第$percent \times M$个元素作为$d_c$。这里$M = \frac 12 N(N-1)$。每个点与剩余的N-1个点都有距离,共$N(N-1)$个距离,取$d_k$作为$d_c$,则一共有$\frac{k}{M}N(N-1)$条边会被统计,平均到每个点上,有$\frac{k}{M}(N-1) \approx \frac{k}{M}N$个邻居,因此,取$k = percent\times M$即可满足论文要求。
$d_c$应该是一个hyperparameter,应当依照经验或其他算法事先选定。
计算点对的时间复杂度和空间复杂度是$N^2$,空间开销过大是一个问题,对于数据量较大的数据集,算法运行所需要的内存太大。可以不事先计算距离,需要的时候在计算,但是时间开销多一项$N^2$。
按照$\rho$从大到小,依据${n_i}$归类。是一种自顶向下的方式。