1. 数据规范化

1.1 数据规范化的作用

不同特征具有不同的量纲，为消除量纲带来的影响，将不同分量的数据都约束在同一范围内，使得指标之间具有可比性或具有相同的权重。
消除离群点、奇异点数据对结果造成的不良影响。
在涉及梯度计算和反向传播的时候，可以加快训练，让损失函数的梯度等高线变得类球形，避免梯度下降轨迹弯弯曲曲（找一个两个自变量的损失函数推一推式子就能得到）。
有可能提高精度（KNN）和收敛性。

1.2 数据规范化的方法

max/min Normalization: 通过线性变化将数据映射到给定的区间范围内，如：

\[\hat v_i = \hat v_{min} + \frac{v_i - v_{min}}{v_{max} - v_{min}} (\hat v_{max} - \hat v_{min})\]

缺点是对离群点敏感，如果有显著的离群点，规范化的效果将会变差。

z-score Normalization

\[\hat v_i = \frac{v_i - \mu}{\sigma}\]

其中$\mu = \frac{1}{n}v_i, \sigma = \sqrt{\frac{1}{n}\sum_{i = 1}^{n}(v_i - \mu)^2}$

将数据分布变化成期望为0，标准差（方差）为1的分布。对离群点不敏感。

非线性归一化。如利用对数函数，指数函数，sigmoid函数，反正切函数。

1.3 应用

概率模型不需要归一化，因为这种模型不关心变量的取值，而是关心变量的分布和变量之间的条件概率；
SVM、线性回归之类的最优化问题需要归一化，是否归一化主要在于是否关心变量取值；
神经网络需要标准化处理，一般变量的取值在-1到1之间，这样做是为了弱化某些变量的值较大而对模型产生影响。一般神经网络中的隐藏层采用tanh激活函数比sigmod激活函数要好些，因为tanh双曲正切函数的取值[-1,1]之间，均值为0.
在K近邻算法中，如果不对解释变量进行标准化，那么具有小数量级的解释变量的影响就会微乎其微。

2. 常见聚类算法

2.1 直接聚类法

是一种基于分层的聚类方法。先将每个点看作一类，每次找距离最近的两类，将他们合并为一类。N个类经过N-1次合并最终变为一类。根据归并的顺序，还可做出谱系图。可以指定距离阈值或聚类个数。

2.2 K-Means

是基于划分的无监督学习算法，是一种迭代的算法。基本思想是将点分配给距离最近的聚类中心，然后根据同一类中的点计算中心，作为新的聚类中心点。

理论分析

K-means基于的一个基本假设是，对于每一个类，可以找到一个中心点，使得这个类中点到这个类的中心点的距离比到其他类的中心点的距离近。

基于这个假设，K-means的损失函数被定义为：

\[\sum_{i = 1}^N \min_{u_j \in C}||x_i - \mu_j||^2 \\ or \\ \begin{aligned} L &= L(X_1, \cdots, X_K, x_i, \cdots, x_N) \\ &= \sum_{k=1}^K\sum_{x_i \in X_k} ||x_i - y_k||^2 \\ \end{aligned}\]

算法分两步：确定${y_k}^K$，分配${x_i}^N$；确定${x_i}^N$，分配${y_k}^K$。

确定${y_k}^K$，分配${x_i}^N$。显然，将$x_i$分配给距离最近的$y_k$即可使损失函数$L$最小。
确定${x_i}^N$，分配${y_k}^K$。利用多元函数微分的知识：

\[\frac{\partial L(X_1, \cdots, X_K, x_i, \cdots, x_N)}{\partial y_k} = \sum_{x_i \in X_k}-2||x_i - y_k||\]

令$\frac{\partial L}{\partial y_k} = 0$，则有：

\[y_k = \frac{1}{|X_k|}\sum_{x_i \in X_k} x_i\]

即，$y_k = center(X_k)$.

每一次迭代，损失函数都只减不增，最后收敛到一个局部最优点。

K-means is equivalent to the expectation-maximization algorithm with a small, all-equal, diagonal covariance matrix.

Time complexity: $O(NKT)$, 其中N是样本数，K是聚类数，T是迭代轮数。

影响结果的因素

K的选取。K-means必须知道K的准确数值才能获得良好的表现。
初始中心点的选取。可以使用L-means++策略选取。
聚类的形状，需要满足基本假设

优缺点

当点是密集且类之前区分明显的情况，表现好；对于大型数据集，该算法可拓展性高，高效。
容易陷入局部最小点。
对离群点敏感，个别离群点在求聚类中心的时候会使得中心点的位置偏离。
只能发现球状的cluster。
inertia不是一个Normalized的指标，在高维空间中欧氏距离会变得很大（维数诅咒）。

2.3 DBSCAN

是一种基于密度的聚类算法，核心思想是计算每个点的邻域内的邻居点数来衡量密度，可以找出不规则形状的聚类，且不需要事先知道聚类数。

基本概念

参数有两个：1. eps($\epsilon$)，指邻域半径；2. MinPts(Minimal number of points required to form clusters, $\mathcal M$)。

考虑数据集$\mathbf X = {x_i}_{i=1}^N$，有如下定义：

点x的$\epsilon$ 邻域

\[N_{\epsilon}(x) = \{x_i|d(x,x_i) \leq \epsilon \}\]

也可以记为：

\[N_{\epsilon}(i) = \{i|d(x,x_i) \leq \epsilon\}\]

密度: $\rho(x) = {| N_{\epsilon}(x)|}$ .
Core point, 点x是core point，当且仅当$\rho(x) \geq \mathcal M$，将所有core points记为$X_c$，并记非核心点为$X_{nc} = X - X_c$.
Border point, 点x是border point（$x \in X_{bd}$），当且仅当$x \in X_{nc}$且$N_{\epsilon}(x) \cap X_c \neq \emptyset$，即非核心点x的邻域包含核心点，或非核心点x落在某个核心点的邻域。
Noise point，点x是noise point，当且仅当$x \in X - (X_c \cup X_{bd})$. 此时$X = X_c \cup X_{bd} \cup X_{noi}$.
Directly density-reachable: 设$x,y\in X$，若$y\in N_{\epsilon}(x)$且$x \in X_c$，则称y是从x直接密度可达的。
Density-reachable: 设$p_1, \cdots, p_m \in X, m \geq 2$，若满足$p_{i+1}$是由$p_i$直接密度可达的，则称点$p_m$是从点$p_1$密度可达。密度可达是直接密度可达的传递闭包。密度可达关系不具有对称性。
Density-connected: 设$x, y, z \in X$，若y,z均是从x密度可达的，则y，z密度相连。密度相连关系具有对称性。
Cluster: 若C是一个cluster，C满足：1.是X的非空子集，2. 若$x \in C$，y从x密度可达（Maximization），则$y \in C$，3. 若$x, y \in C$，则x和y密度相连（Connectivity）。

算法流程

该算法中，边界点的归属会受点的遍历顺序的影响。如果边界点的归属很重要，可以先将边界点标记出来，在最后分配给最近的类。

问题

$\epsilon$的选取。是一个固定的、统一的值，在过密的点中容易将多个聚类当作一类，在过疏的点中容易将一类分散成多类。对数据点的适应度不够。
参数$\mathcal M$的选择。$\mathcal M$有一个指导性原则，即$\mathcal M \geq dim+1$.
复杂度问题。时空复杂度为$O(N^2)$，可用kd tree等索引结构降为$O(NlogN)$ .
距离公式的选取。如果选用欧几里得距离，在维数增大的时候，由于curse of dimensionality，很难选到一个合适的$\epsilon$值。

2.4 OPTICS

可以看作对DBSCAN的一种改进，使得DBSCAN对参数不那么敏感。 OPTICS不直接给出聚类结果，而是给出一个有序数组，包含了可以用来做聚类的信息。其中信息也可以用来做关联分析等。

基本概念

大部分概念和DBSCAN一致。另给出两个概念：

Core distance，核心距离。设$x \in X$，使得x称为核心点的最小邻域半径为x的核心距离。

\[cd(x) = \left\{ \begin{array}{rcl} Undefined & |N_{\epsilon}(x) < \mathcal M| \\ d(x, N_{\epsilon}^{\mathcal M}(x) & |N_{\epsilon}(x) \geq \mathcal M| \end{array}\right.\]

其中$N_{\epsilon}^{i}(x)$指点x邻域中x距离第i近的点的距离。如果x本身是核心点，则$cd(x) \leq \epsilon$.

Reachable distance，可达距离。设$x, y \in X$，对于给定的参数$\epsilon$和$\mathcal M$，y关于x的可达距离为：

\[rd(y,x) = \left\{ \begin{array}{rcl} Undefined & |N_{\epsilon}(x) < \mathcal M| \\ \max\{d(x, y), cd(x)\} & |N_{\epsilon}(x) \geq \mathcal M| \end{array}\right.\]

特别的，当x是核心点时，y关于x的可达距离可以理解为：使得x是核心点且y是从x直接密度可达的点的最小邻域半径。注： $rd(y,x)$的值与y所在空间的密度有关，密度越大，它从相邻节点直接密度可达的距离就越小．如果聚类时想要朝着数据尽量稠密的空间进行扩张，那么可达距离最小的点是最佳的选择．为此，OPTICS算法中用一个可达距离升序排列的有序种子队列存储待扩张的点，以迅速定位稠密空间的数据对象.

上面的算法处理完后，我们得到了输出结果序列，每个节点的可达距离和核心距离。我们以可达距离为纵轴，样本点输出次序为横轴进行可视化：

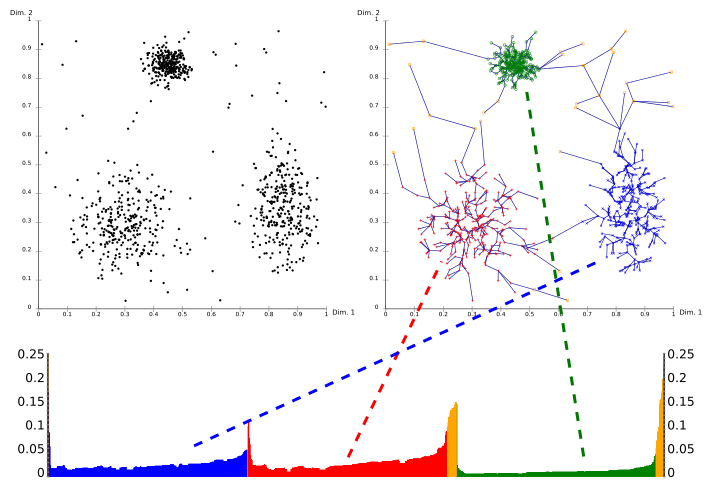
x轴为输出序列p的点的编号，y轴是可达距离。

簇在坐标轴中表述为山谷，并且山谷越深，簇越紧密。

黄色代表的是噪声，它们不形成任何凹陷。

OPTICS的核心思想：1) 较稠密簇中的对象在簇排序中相互靠近，2)一个对象的最小可达距离给出了一个对象连接到一个稠密簇的最短路径。相对于DBSCAN，该算法对于距离阈值$\epsilon$的敏感性大大降低，这是因为：

在OPTICS算法中从输出得到的并不是直接的聚类结果，而是在$\epsilon$和$\mathcal M$下的有序队列，以及所有样本点的核心距离和可达距离。
在处理结果队列时，通过判断样本点的核心距离是否小于等于$\epsilon$实际上就是在判断该样本点是否是新半径$\epsilon^{‘}$的核心点，其中$\epsilon^{‘} < \epsilon$。而两者都不满足的样本点一定会被认为是噪声，所以对于距离阈值，该算法有一定的不敏感性。

OPTICS相当于将$\epsilon$改为动态的DBSCAN算法，可以进行多密度的聚类（因为ϵ$\epsilon$对于结果的影响较低，且输出中包含了关于可达距离的信息，可以辅助设置$\epsilon$) 综上，OPTICS可以在minPts固定的前提下，对于任意的$\epsilon^{‘}$(其中$\epsilon^{‘} \leq \epsilon$)都可以直接经过简单的计算得到新的聚类结果。直观从结果图来看，以某一个可达距离$\epsilon$画平行于x轴的直线，当直线穿过几个山谷区域，最终就会得到几种簇（因为每一个山谷代表一种簇，或说一团高密度区域）。在此基础上，我们可以选择合适的可达距离$\epsilon$做为其它距离算法（例如DBSCAN）的初始参数设定从而进行聚类。从这个角度来看，OPTICS聚类算法也可以被认为是一种筛选最优距离阈值$\epsilon$的方法。